本博客日IP超过2000,PV 3000 左右,急需赞助商。
极客时间所有课程通过我的二维码购买后返现24元微信红包,请加博主新的微信号:xttblog2,之前的微信号好友位已满,备注:返现
受密码保护的文章请关注“业余草”公众号,回复关键字“0”获得密码
所有面试题(java、前端、数据库、springboot等)一网打尽,请关注文末小程序
腾讯云】1核2G5M轻量应用服务器50元首年,高性价比,助您轻松上云
今天为大家分享一道关于“电灯泡”的题目。
话不多说,直接看题。
初始时有 n 个灯泡关闭。第 1 轮,你打开所有的灯泡。第 2 轮,每两个灯泡关闭一次。第 3 轮,每三个灯泡切换一次开关(如果关闭则开启,如果开启则关闭)。第 i 轮,每 i 个灯泡切换一次开关。对于第 n 轮,你只切换最后一个灯泡的开关。找出 n 轮后有多少个亮着的灯泡。
www.xttblog.com
示例:
输入: 3
输出: 1
解释:
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭].
你应该返回 1,因为只有一个灯泡还亮着。
这是一道难度评定为困难的题目。但是,其实这并不是一道算法题,而是一个脑筋急转弯。只要我们模拟一下开关灯泡的过程,大家就会瞬间get,一起来分析一下:
我们模拟一下n从1到12的过程。在第一轮,你打开了12个灯泡:

因为对于大于n的灯泡你是不care的,所以我们用黑框框表示:

然后我们列出n从1-12的过程中所有的灯泡示意图:
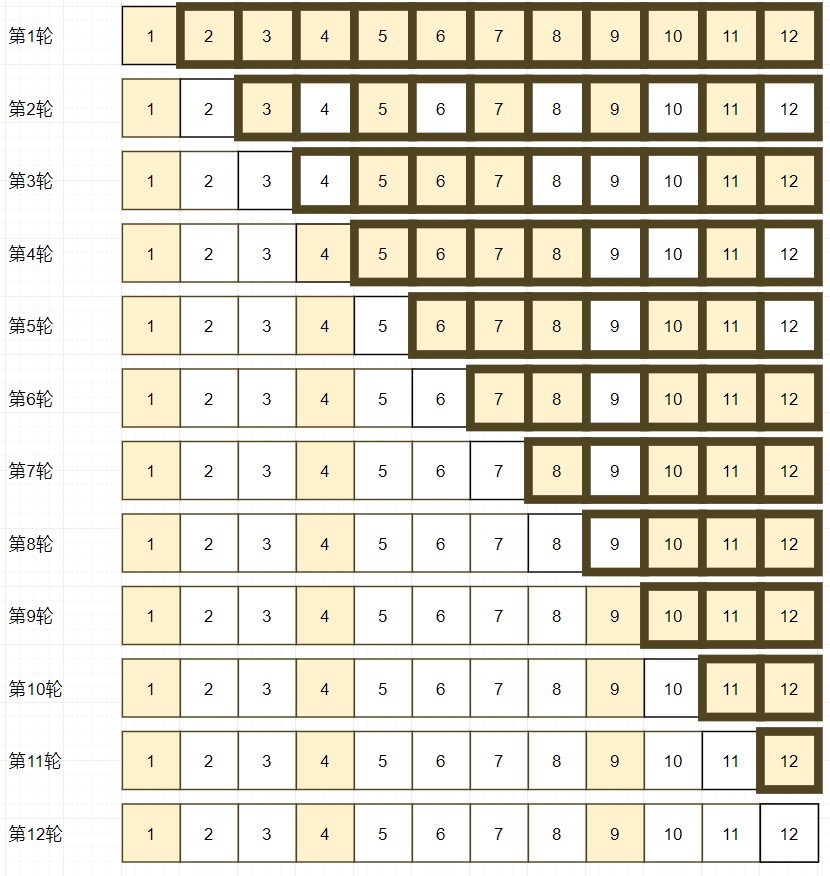
可以得到如下表格:
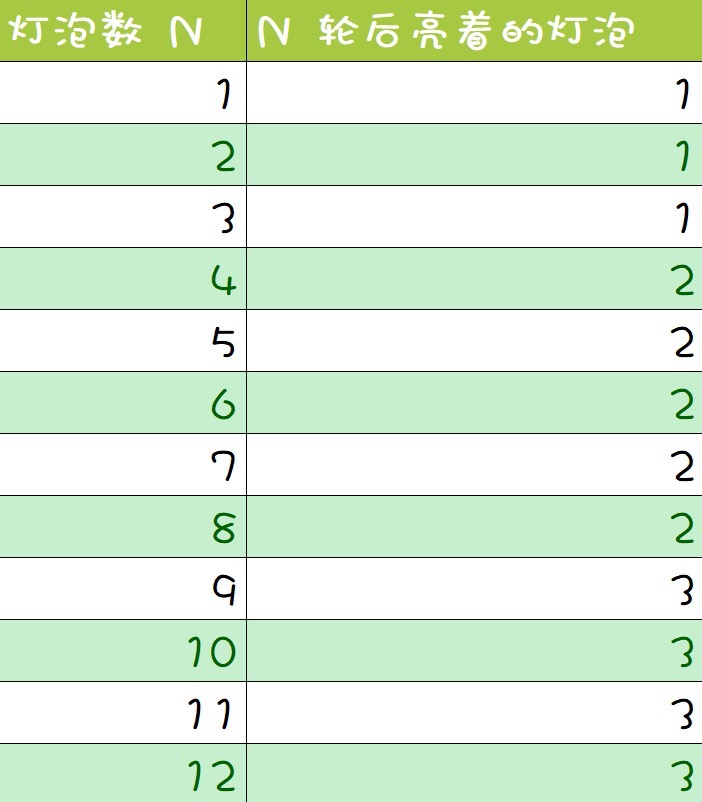
观察一下,这是什么?观察不出来,咱们看看这个:
//go
func main() {
for n := 1; n <= 12; n++ {
fmt.Println("n=", n, "\t灯泡数\t", math.Sqrt(float64(n)))
}
}上面代码是用 go 实现的,大家也可以使用 Java 来实现。
//print
n= 1 灯泡数 1
n= 2 灯泡数 1.4142135623730951
n= 3 灯泡数 1.7320508075688772
n= 4 灯泡数 2
n= 5 灯泡数 2.23606797749979
n= 6 灯泡数 2.449489742783178
n= 7 灯泡数 2.6457513110645907
n= 8 灯泡数 2.8284271247461903
n= 9 灯泡数 3
n= 10 灯泡数 3.1622776601683795
n= 11 灯泡数 3.3166247903554
n= 12 灯泡数 3.4641016151377544没错,只要我们对n进行开方,就可以得到最终的灯泡数。根据分析,得出代码:
//给一个c++版本的
class Solution {
public:
int bulbSwitch(int n) {
return sqrt(n);
}
};
也可能有人对上面的结果表示不服,没有证明,你说毛线!证明如下:
约数,又称因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数,我们就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的约数。
从我们观察可以发现,如果一个灯泡有奇数个约数,那么最后这个灯泡一定会亮着。
什么,你问我奇数是什么?奇数(odd)指不能被2整除的整数 ,数学表达形式为:2k+1, 奇数可以分为正奇数和负奇数。
所以其实我们是求,从1-n有多少个数的约数有奇数个。而有奇数个约数的数一定是完全平方数。这是因为,对于数n,如果m是它的约数,则n/m也是它的约数,若m≠n/m,则它的约数是以m、n/m的形式成对出现的。而m=n/m成立且n/m是正整数时,n是完全平方数,而它有奇数个约数。
我们再次转化问题,求1-n有多少个数是完全平方数。
什么,你又不知道什么是完全平方数了?完全平方指用一个整数乘以自己例如11,22,3*3等,依此类推。若一个数能表示成某个整数的平方的形式,则称这个数为完全平方数。
到这里,基本就很明朗了。剩下的,我想不需要再说了吧!

最后,欢迎关注我的个人微信公众号:业余草(yyucao)!可加作者微信号:xttblog2。备注:“1”,添加博主微信拉你进微信群。备注错误不会同意好友申请。再次感谢您的关注!后续有精彩内容会第一时间发给您!原创文章投稿请发送至532009913@qq.com邮箱。商务合作也可添加作者微信进行联系!
本文原文出处:业余草: » 漫画算法:骚操作系列(灯泡开关的经典面试题)
